Editor's Note: This essay is redacted from Prescott's 2004 Nobel Prize Address in Economics, delivered at Stockholm University in December 2004. Prescott was a co-recipient of the prize, along with Finn E. Kydland of Carnegie Mellon University in Pittsburgh and the University of California, Santa Barbara. They were awarded "for their contributions to dynamic macroeconomics: the time consistency of economic policy and the driving forces behind business cycles." A more complete paper based on Prescott's address is forthcoming in the Journal of Political Economy and on the Nobel Prize Committee's Web site.
What I am going to describe for you is a revolution in macroeconomics, a transformation in methodology that has reshaped how we conduct our science.
Prior to the transformation, macroeconomics was largely separate from the rest of economics. Indeed, some considered the study of macroeconomics fundamentally different and thought there was no hope of integrating macroeconomics with the rest of economics, that is, with neoclassical economics. Others held the view that neoclassical foundations for the empirically determined macro relations would, in time, be developed. Neither view proved correct.
Finn E. Kydland and I have been lucky to be a part of this revolution, and my address will focus heavily on our role in advancing this transformation. Now, all stories about transformation have three essential parts: the time prior to the key change, the transformative era, and the new period that has been impacted by the change. And that is the story I am going to tell: how macroeconomic policy and research evolved from a system of equations to an investigation of dynamic stochastic economies. In other words, this is a story about how the macroeconomy finally came alive for macroeconomists.
Before proceeding, I want to emphasize that the methodology that transformed macroeconomics, which used to be the study of business cycle fluctuations, is applicable to the study of virtually all fields of economics. In fact, the meaning of the word macroeconomics has changed to refer to the tools being used rather than to the study of business cycle fluctuations.
These are exciting times in macroeconomics. The methodology that Finn Kydland and I developed for the study of business cycle fluctuations is being used to advance learning not only in the area of business cycles, but also in virtually all areas of economics. By using this methodology, researchers are able to apply theory and measurement to answer questions, define puzzles, and determine where better measurement is needed before specific questions can be answered.
For example, over the past five years I have been addressing the following questions using this methodology:
- What is the fundamental value of the stock market, and do fundamentals account for the large movements in the value of the stock market?
- Why did hours worked per adult fall by one-third in Western Europe, and not in Canada and the United States, in the 1970-1995 period?
- Why were market hours in the United States at the end of the 1990s 5 percent above what theory predicts?
- Why did Japan lose a decade of growth beginning in 1992, a decade when growth was at trend in the other advanced industrial countries?
Much of this recent research originates from my undergraduate teaching that began in the late 1990s. Until then, I had never taught a course in which economic questions were addressed using this methodology. The undergraduate course I taught was Quantitative Analysis of the Macroeconomy. I chose to teach this course because I felt there was a need to develop material that could be used in teaching what macroeconomics has become at the undergraduate level. I felt there was a need because Finn's and my work on the time consistency problem and developments in agency theory led me to the conclusion that having good macroeconomic policy requires having an educated citizenry that can evaluate macroeconomic policy. Macroeconomic policy is too important to be left to those who claim expertise in the subject.
Macroeconomics has progressed beyond the stage of searching for a theory to the stage of deriving the implications of theory. In this way, macroeconomics has become like the natural sciences. Unlike the natural sciences, though, macroeconomics involves people making decisions based upon what they think will happen, and what will happen depends upon what decisions they make. This means that the concept of equilibrium must be dynamic, and—as we shall see—this dynamism is at the core of modern macroeconomics.
The Transformation of Macroeconomic Policy
Before the transformation of macroeconomic policy, what was evaluated was a policy action given the current situation. Economists were busy trying to understand the determinants of output at a particular point in time; if they could discern those factors, they could suggest a policy to tweak the economy and to attain the desired output and thus tame the business cycle. After the transformation of macroeconomic policy, economists now consider the whole structure of business cycles and their many characteristics, and rather than an action, what is evaluated is a policy rule.
However, it turns out that there is no best policy rule. I will have more to say about this seeming incongruity in a moment. For now, let me note that any policy rule that is best, given that it will be followed in the future, is by definition time consistent, but—except in empirically uninteresting cases—time consistent rules are not optimal. Why? As we shall see, following a rule that makes sense in the short run (time consistency) may have deleterious long-run effects. This puts a premium on following good rules. All that can be hoped for is to follow a good rule, and this requires institutions that sustain this rule.
Macroeconomic Models Before the Transformation
Macroeconomic models were systems of equations that determined current outcomes given the values of the current policy actions, values of predetermined variables, and values of any stochastic shocks. Thus, physical models and pretransformation macro models have the same mathematical structure. With the system-of-equations approach, each equation in the system was determined up to a set of parameters. In the simple prototype macroeconometric model, there were a consumption function, an investment equation, a money demand function, and a Phillips curve. Behind all these equations were a rich empirical literature and, in the case of the consumption function, money demand function, and investment equation, some serious theoretical work. These models were notable in that they ignored the decision as to how much time to allocate to the market. The final step was to use the tools of statistical estimation theory to select the parameters.
I worked in this tradition. In my dissertation, I formulated the optimal policy selection problem as a Bayesian sequential decision problem (which, simply described, is a mathematical means of dealing with uncertainty in dynamic decision-making situations). This type of work was expected of a young scholar if he hoped to be taken seriously. Macroeconometric models organized the field, and success in macroeconomics was to have your equation incorporated into one of these models. Indeed, Robert E. Lucas Jr. and I were searching for a better investment equation in 1969 when we wrote our paper "Investment Under Uncertainty" (1971).
A key assumption in the system-of-equations approach is that the equations are policy invariant. As Lucas (1976) points out in his critique, which was presented in 1973, this assumption is inconsistent with dynamic economic theory. His insight made it clear that there was no hope for the neoclassical synthesis—that is, the development of neoclassical underpinnings of the system-of-equations macro models.
Fortunately, with the development of dynamic economic theory, the language of general equilibrium theory, and recursive methods, an alternative set of tractable macro models was developed for drawing scientific inference.
Macroeconomic Models After the Transformation
Models after the transformation are dynamic, fully articulated model economies in the general equilibrium sense of the word economy. Model people maximize utility given the price system, policy, and their consumption possibility set; firms maximize profits given their technology set, the price system, and policy; and markets clear. The key assumption is that preferences and technology are invariant to policy. They are the data of the theory and not the equations as in the system-of-equations approach. To repeat, with the general equilibrium approach, empirical knowledge is organized around preferences and technology, not around some set of equations.
The Time Inconsistency of Optimal Policy
Before the transformation, optimal policy selection was a matter of solving what the physical scientists called a control problem. This is not surprising, given that the system-of-equations approach was borrowed from the physical sciences. With such systems, the principle of optimality holds—that is, it is best to choose at each point in time what is best given the current situation and the rules by which policy will be selected in the future. The optimal policy is time consistent, and dynamic programming techniques can be used to find the optimal policy as in the physical sciences. This is true even if uncertainty exists.
However, Finn Kydland and I had read the Lucas critique and knew that for dynamic equilibrium models, only policy rules could be evaluated. This led us to search for a best rule to follow, where a rule is a function that specifies policy actions as a function of the state or position of the economy. We had worked on this problem before Finn left Carnegie Mellon to join the faculty of the Norwegian School of Business and Economics in 1973. In academic year 1974-1975, I visited the Norwegian School of Business and Economics, and in the spring of 1975, Finn and I returned to this problem. In previous research we had considered time consistent stationary policy rules. These rules have the property that they are a fixed point of the mapping that specifies the best rule today as a function of the rule that will be used in the future.
The fact that these rules were not optimal led us to our key insight: The best event-contingent policy plan is not time consistent. By this I mean that the continuation of a plan at some future point in the event-time tree is not optimal. This leads to the conclusion that there is value in being able to commit and that there are costs to having discretion. The only method of commitment is to follow rules. That is why we concluded that the time inconsistency of optimal plans necessitates following rules. Some societies have had considerable success in following good, but time inconsistent, policy rules. Other societies have had limited success in this regard and, as a result, their citizens suffer.
This need for rules in organizational settings has long been recognized. That is why all agree that rule by a good set of laws is desirable. This rule by law is a political institution to get around this time consistency problem. As we shall now see, what was new in our research was that this principle also holds for macroeconomic policy, which was counter to what most people thought at the time.
The Low Inflation Rule and an Independent Central Bank
A notable example of a success in following a good, but time inconsistent, rule is the one maintaining a low and stable inflation rate. Before describing an institution that is proving effective in getting commitment to this good rule in many countries, I will first describe why the price stability policy rule is time inconsistent.
In the economy considered, the nominal wage rate is set above the market-clearing level in some sectors, given the inflation rate specified by the rule. This outcome could be the result of industry insiders in each of a number of industries finding this rule optimal, given the wages chosen by the insiders in other industries and the expected inflation rate. If this rule is followed, ex post a distortion occurs that results in low employment. This distortion can be reduced by having inflation in excess of the amount specified by the rule. With the time consistent monetary policy rule, inflation will be at that level where the marginal value of higher inflation in reducing the distortion will just equal the marginal cost of the higher inflation. The equilibrium outcome is high inflation and no reduction in the distortion. Commitment to the best rule will not result in high inflation, just the labor market distortion.
I turn now to an institution that is proving successful in sustaining this rule. This institution is an independent central bank. Members of this organization have a vested interest in following this rule, for if it is not followed they would incur the risk that they would suffer in the future. If inflation has been excessive and a new administration is elected, top people in the organization will be replaced and the size of the central bank cut. Thus, members of this organization have a vested interest in the rule being followed.
The increased stability of the economy and the improved performance of the payments and credit system may be due, in part, to the diffusion of findings of Finn's and my "Rules Rather Than Discretion" paper. People now recognize much better the importance of having good macroeconomic institutions such as an independent central bank.
During the 1981 and current oil crises, for example, I was pleased that policies were not instituted that adversely affected the economy by reducing production efficiency. This is in sharp contrast to the oil crisis in 1974 when, rather than letting the economy respond optimally to a bad shock so as to minimize its cost, policies were instituted that adversely affected production efficiency and depressed the economy much more than it would otherwise have been.
Finn and I found that responses to both bad and good shocks are optimal and that attempts at stabilization policy are counterproductive. Now, when I say that responses to shocks are optimal, I am referring to market responses. What policy should focus on are the big things, such as what is a good tax system, what should be the level of government-provided services, and what policies are best given both positive and negative externalities.
The Transformation of Macroeconomic Research
The title of this address is "The Transformation of Macroeconomic Policy and Research." I turn now to the research part of the title. The methods used in macroeconomic research were different prior to Finn's and my paper, "Time to Build and Aggregate Fluctuations" (1982). The new methodology was developed in the summer of 1980 when Finn and I did the research for our "Time to Build" paper. We also wrote the first draft of this paper that summer.
Before specifying the new research methodology, I have to discuss what the key business cycle facts are and why they led economists to falsely conclude that business cycle fluctuations were not in large part equilibrium responses to real shocks, as conjectured by Knut Wicksell (1907) and Arthur C. Pigou (1927). Then I will describe the methodology that Finn and I developed and used to quantitatively determine the consequences of these shocks for business cycle fluctuations.
I emphasize that what is important is the methodology, and that this methodology can be, and has been, used to quantitatively determine the consequences of both nominal and real shocks. By using these methods, the profession has learned so much. No longer do economists conjecture and speculate. Instead they make quantitative statements as to the consequences of various shocks and features of reality for business cycle fluctuations. This paper began a constructive and fruitful research program.
Business Cycle Facts
In the 1970s, after the development of dynamic economic theory, it was clear that something other than the system-of-equations approach was needed if macroeconomics was to be integrated with the rest of economics. I want to emphasize that macroeconomics then meant business cycle fluctuations. Growth theory, even though it dealt with the same set of aggregate economic variables, was part of what was then called microeconomics, as was the study of tax policies in public finance.
Business cycles are fluctuations in output and employment about trend. But what is trend? Having been trained as a statistician, I naturally looked to theory to provide the definition of trend, with the plan to then use the tools of statistics to estimate or measure it. But theory provided no definition of trend, so Robert J. Hodrick and I in 1978 took the then-radical step of using an operational definition of trend.1 With an operational definition, the concept is defined by the procedure used to determine the value of the concept.
Our trend is just a well-defined statistic, where a statistic is a real valued function. Hodrick and Prescott's (1980) trend statistic mimics well the smooth curve that economists fit through the data. The family of trends we considered is one-dimensional. The one in the family that we used is the first one we considered. Later we learned that the actuaries use this family of smoothers, as did John von Neumann when he worked on ballistic problems for the U.S. government during World War II.2 A desirable feature of this definition is that with the selection of smoothing parameters for quarterly time series, there are no degrees of freedom and the business cycle statistics are not a matter of judgment. Having everyone looking at the same set of statistics facilitated the development of business cycle theory by making studies comparable.
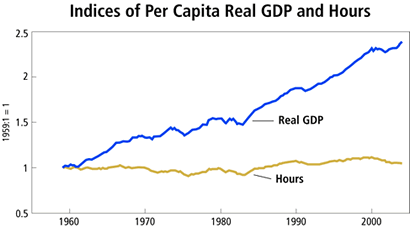
One set of key business cycle facts is that two-thirds of business cycle fluctuations are accounted for by variations in the labor input, one-third by variations in total factor productivity, and virtually zero by variations in the capital service input. Total factor productivity, or TFP, represents output growth that is not accounted for by growth in inputs; that is, it is the rate of transformation of total input into total output. The importance of variation in the labor input can be seen in Figure 1 This is in sharp contrast to the secular behavior of output and the labor input, which is shown in Figure 2. Secularly, per capita output has a strong upward trend, whereas the per capita labor input shows no trend.
Figure 1
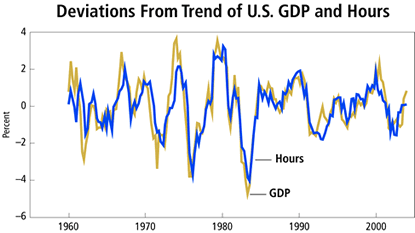
Figure 2
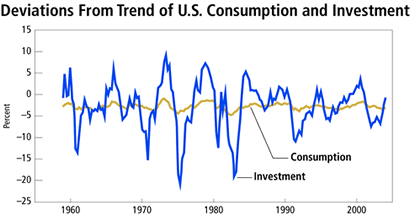
A second business cycle fact is that consumption moves procyclically; that is, the cyclical component of consumption moves up and down with the cyclical component of output. A third fact is that in percentage terms, investment varies 10 times as much as does consumption. Consequently, investment variation is a disproportionate part of cyclical output variation. This is shown in Figure 3.
Figure 3
Inference Drawn From These Facts
Now why did economists looking at these facts conclude that they ruled out total factor productivity and other real shocks as being significant contributors to business cycle fluctuations? Their reasoning is as follows. Leisure and consumption are normal goods. The evidence at that time was that the real wage was acyclical, which implies no cyclical substitution effects and leaves only the wealth effect. Therefore, in the boom when income is high, the quantity of leisure should be high, which is not the case. This logic is based on partial equilibrium reasoning, and the conclusion turned out to be wrong.
In the 1970s a number of interesting conjectures arose as to why the economy fluctuates as it does. Most were related to finding a propagation mechanism that resulted in Lucas' monetary surprise shocks having persistent real effects. With this theory, leisure moves countercyclically in conformity with observations. But the deviations of output and employment from trend are not persistent with this theory, which is at variance with observations. This initiated a search for some feature of reality that when introduced gives rise to persistent real effects. To put it another way, economists searched for what Ragnar Frisch called a propagation mechanism for the effects of monetary surprises.
Macroeconomics and Growth Theory Before the "Time to Build" Paper
Macroeconomics of the 1970s largely ignored capital accumulation. Growth theory was concerned with the long-term movements in the economic aggregates, while macroeconomics was concerned with the short-term movements. Virtually no connection was made between the then-dormant growth theory and the dynamic equilibrium theories of business cycles. The reason probably was that short-term movements in output are accounted for in large part by movements in the labor input, while long-term growth in living standards is accounted for by increases in per capita capital service input and in total factor productivity.
Finn Kydland and I decided to use the neoclassical growth model to study business cycle fluctuations in the summer of 1980. The basic theoretical framework we developed came to be called the real business cycle model. The term real does not mean that the framework can be used only to answer questions concerning the consequences of real shocks. The real business cycle model is equally applicable to addressing the consequences of monetary shocks. As I said before, I will not be discussing these monetary applications in this address because Finn will in his address. This is appropriate given that he and his collaborators, and not I, are the leaders in the study of the consequences of monetary policy for business cycles.
The Methodology
This model builds on the contributions of many economists, many of whom have been awarded the Nobel Prize. The importance of the contributions of Simon Kuznets and Richard Stone in developing the national income and product accounts cannot be overstated. These accounts reveal a set of growth facts, which led to Robert M. Solow's (1956) classical growth model, which Solow (1970) calibrated to the growth facts. This simple but elegant model accounts well for the secular behavior of the principal economic aggregates. With this model, however, labor supply is supplied inelastically and savings is behaviorally determined. There are people in the classical growth model economy, but they make no decisions. This is why I, motivated by Ragnar Frisch's Nobel address delivered here in 1969, refer to this model as the classical growth model.
In the full paper forthcoming from this address, I go to great lengths to describe the eight steps involved in this methodology. In essence, those eight steps lay the groundwork for creating models from which we can derive the quantitative implications of theory. For the first time, these models marry the micro with the macro by incorporating utility-maximizing consumers, profit-maximizing firms, and markets clearing. With this methodology, models aren't a static endgame, as they are under the system-of-equations approach; rather, with this new methodology, models become a dynamic means for understanding the economy.
Using the Methodology in Business Cycle Research
As reported in our paper "Time to Build and Aggregate Fluctuations" (1982), Finn Kydland and I found that if elasticity of substitution of labor supply is 3 (in other words, that labor supply is highly elastic), and that if TFP shocks are highly persistent and of the right magnitude, then business cycles are what the neoclassical growth model predicts. This includes the amplitude of fluctuation of output, the serial correlation properties of cyclical output, the relative variability of consumption and investment, the fact that capital stock peaks and bottoms out later than does output, the cyclical behavior of the labor input, and the cyclical output accounting facts.
Subsequently, I found that the shocks were highly persistent and the TFP shocks of the right magnitude (1986). Conditional on a labor supply elasticity close to 3, TFP shocks are the major contributor to fluctuations in the period 1954-1981 in the United States. This finding turned out to be highly robust, and there are a number of examples where economists today are using this methodology to confirm this result (which, again, is described at length in my forthcoming paper). In all these cases, to generate business cycles of the magnitude and nature observed, the aggregate labor supply elasticity must be 3. This attests to the robustness of the finding and focuses attention on this parameter. A variety of evidence must be considered that supports the number 3 before it is safe to conclude that the neoclassical growth model predicts business cycle fluctuations of the nature observed.
Evidence That the Aggregate Elasticity of Labor Supply Is 3
A problem with the abstraction that many economists used to incorrectly conclude that labor supply is inelastic is that it has the prediction that everyone should make essentially the same percentage adjustment in hours worked. This is not the case. Over the business cycle, most of the variation in the aggregate number of hours worked is in the fraction of people working and not in the hours worked per worker. Looking at this observation, Richard Rogerson (1984, 1988) studies a static world where people either work a standard workweek or do not work. He shows that in this world, the aggregate elasticity
of labor supply is infinite up to the point that the fraction employed is one.
Rogerson's aggregation result is every bit as important as the one giving rise to the aggregate production function.3 In the case of production technology, the nature of the aggregate production function in the empirically interesting cases is very different from that of the individual production units being aggregated. The same is true for the empirically interesting cases in which households are aggregated into an aggregate or a stand-in household.
Recent Evidence From Consequences of Tax Rates
Across Countries and Across Time
Good statistics are available on labor supply and tax rates across the major advanced industrial countries. My measure of aggregate labor supply is aggregate hours worked in the market sector divided by the number of working-age people.
Given that the effect of the marginal effective tax rate on labor supply depends on this elasticity, and given that tax rates vary considerably, these observations provide an almost ideal test of whether the aggregate labor supply elasticity is 3. The set of countries that Prescott (2004) studies is the G-7 countries, which are the large advanced industrial countries. The differences in marginal tax rates and labor supply are large: Canada, Japan, and the United States have rates near 0.40, and France, Germany, and Italy near 0.60. (See Prescott 2004.) The prediction, based on an aggregate labor supply elasticity of 3, that Western Europeans will work one-third less than North Americans and Japanese is confirmed.4 Added evidence for an aggregate elasticity of 3 is that it explains why labor supply in France and Germany was nearly 50 percent greater during the 1970-1974 period than it is today.
Observations on aggregate labor supply across countries and across time imply a labor supply elasticity near 3, and additional evidence is provided in my forthcoming paper.
Beyond Business Cycle Research
The methodology that Finn Kydland and I developed and used to study business cycles is equally applicable to studying other phenomena. In the process of using the theory to answer other economic questions, the theory is being tested. In this section I will briefly review three successful applications of this methodology and one very interesting open puzzle. While presenting evidence that the labor supply elasticity is 3, I have already effectively reviewed one highly successful application—namely, my study assessing the role of taxes in accounting for the huge differences in labor supply across the advanced industrial countries and the huge fall in labor supply in Europe between the early 1970s and the mid-1990s.
Using the Methodology in the Stock Market Valuation Research
An interesting question is, Why did the value of the stock market relative to GDP vary by a factor of 2.5 in the United States and 3 in the United Kingdom in the last half of the 20th century? Other variables display little secular variation relative to GDP, whether they are corporate after-tax profits or corporate physical capital relative to GDP.
Clearly, the single-sector neoclassical growth model does not suffice for studying the market value of corporate equity. There must be both a corporate and a noncorporate sector. Fortunately, the national accounts report the components of value added for the corporate sector as well as for government business, household business, and unincorporated business sectors. Various adjustments must be made to the accounts so that they are in conformity with the model, such as using producer prices for both inputs and outputs in the business sector.
In an equilibrium relation, the market value of corporations is equal to the value of their productive assets. The capital accounts of the national accounts provide measures of the cost of replacing tangible capital. But corporations also own large amounts of intangible capital, including organization capital, brand names, and patents, which also affect the market value of corporations. These assets cannot be ignored when determining what theory says the value of the stock market should be. This presents a problem for determining the fundamental value of the stock market—a problem that Ellen R. McGrattan and I solve. (See McGrattan and Prescott 2005a.)
We find that the secular behavior of the value of the U.S. stock market is as theory predicts. What turns out to be important for the movement in the value of corporations relative to GDP are changes in tax and regulatory policies. If the tax rate on distributions by corporations is 50 percent rather than 0 percent, the value of corporations will be only half as large given the resource cost of their productive assets.
Our study uses a neoclassical growth model and connects the model to national income and product data, tax data, and sector balance sheet data. We submitted the paper to the Review of Economic Studies, a British journal. The editor rightfully insisted that we do the analysis for the U.K. stock market as well as the U.S. stock market. We were nervous as to what theory and data would say, and we were happy when we found that the behavior of the value of the U.K. stock market also was in conformity to theory. Here is an example of the power of the macroeconomic methodology that Finn and I developed.
The excessive volatility of stock prices remains. Indeed, our study strengthens this puzzle. Stocks of productive capital vary little from year to year while stock prices sometimes vary a lot. I am sure this volatility puzzle will, in the not too distant future, be resolved by some imaginative neoclassical economist. However, resolving the secular movement puzzle is progress.
This example illustrates how macroeconomics has changed as a result of the methodology that Finn and I pioneered. It is now that branch of economics where applied dynamic equilibrium tools are used to study aggregate phenomena. The study of each of these aggregate phenomena is unified under one theory. This unification attests to the maturity of economic science when it comes to studying dynamic aggregate phenomena.
Using the Methodology to Study the U.S. Great Depression
The welfare gains from eliminating business cycles are small or negative. The welfare gains from eliminating depression and creating growth miracles are large. Harold L. Cole and Lee E. Ohanian (1999) broke a taboo and used the neoclassical growth model to study the U.S. Great Depression. One of their particularly interesting findings is that labor supply on a per adult basis in the 1935-1939 period was 25 percent below what it was before the Depression. Recently, Cole and Ohanian (2004) used neoclassical economics to show how New Deal cartelization could very well have been the reason for the low labor supply. The rapid recovery of the U.S. economy subsequent to the abandonment of these cartelization policies supports their theory.
Japan's Lost Decade of Growth
A more recent example is Japan's lost decade of growth, which was the 1992-2001 period. Fumio Hayashi and Prescott (2002), treating TFP as exogenous, find that the neoclassical growth model predicts well the path of the principal aggregates. In particular, it quantitatively predicts the large capital deepening and the associated fall in the return on capital. It quantitatively predicts the behavior of labor supply as well, which is further evidence for the high elasticity of labor supply.
A Business Cycle Puzzle
An economic boom in the United States began with an expansion in early 1996 and continued to the fourth quarter of 1999. Then a contraction set in and continued until the third quarter of 2001. At the peak, detrended GDP per working-age person was 4 percent above trend and labor supply 5 percent above average. None of the obvious candidates for the high labor supply was operating. There was no war with temporarily high public consumption that was debt-financed, tax rates were not low, TFP measured in the standard way was not high, and there was no monetary surprise that would give rise to high labor supply. This is why I say this boom is a puzzle for the neoclassical growth model.
Why did people supply so much labor in this boom period? The work of McGrattan and Prescott (2005a), which determines the quantitative predictions of theory for the value of the stock markets, suggests a resolution. The problem is one of measurement. During this period there is evidence that unmeasured investment was high, as was unmeasured compensation (McGrattan and Prescott 2005b). Therefore, output and productivity were higher than the standard statistics indicate. The measurement problem is to come up with estimates of this expensed investment. With these improved measurements of economic activity, theory can be used to determine whether the puzzle has been solved.
This example illustrates the unified nature of aggregate economics today. The real business cycle model was extended and used to understand the behavior of the stock market, and that extended model in turn is now being used to resolve a business cycle puzzle.
Ragnar Frisch's Vision Realized
I conclude this address with an ode to Ragnar Frisch, who, along with Jan Timbergen, was one of the first to be awarded the Nobel Prize in 1969. Frisch's Nobel address is titled "From Utopian Theory to Practical Applications: The Case of Econometrics" (1970). He is the father of quantitative neoclassical economics, which is what he is referring to by the word econometrics in the title.5 This is not what the word econometrics means today, but given that Frisch invented the word, he had every right to use it as he does.
Prior to Frisch's creating the Econometric Society in 1930 and launching Econometrica in 1933, neoclassical economists did little to verify their theoretical results by statistical observations. Frisch writes in his Nobel address that the reason was in part the poor quality of statistics then available and in part that neoclassical theory was not developed with systematic verification in view. The American Institutionalists and German Historical schools pointed this out and advocated letting the facts speak for themselves. The impact of these schools on economic thought was minimal. To quote Frisch, "Facts that speak for themselves talk in a very naïve language" (1970, p. 16). Now theory derives its concepts from measurement, and in turn theory dictates new measurement. The latter is what McGrattan and I are currently doing to resolve the puzzle of why U.S. employment was so high at the end of the 1990s.
In the 1960s Frisch was frustrated by the lack of progress in his quest to make neoclassical economics quantitative and referred to much of what was being done then as "playometrics." It is a little unfair to criticize those studying business cycles at that time for not using the full discipline of neoclassical economics. All the needed tools were not yet part of the economist's tool kit. Some of these tools that are crucial to the study of business cycles are James Savage's statistical decision theory, as uncertainty is central to business cycles; Kenneth J. Arrow's and Gerard Debreu's extension of general equilibrium theory to environments with uncertainty; David Blackwell's and others' development of recursive methods, which are needed in computation and in representation of a dynamic stochastic equilibrium; Lucas and Prescott's (1971) development of recursive competitive equilibrium theory;6 and, of course, the computer.
Particularly noteworthy is Lucas' role in the macroeconomic revolution. In the very early 1970s, he revolutionized macroeconomics by taking the position that neoclassical economics can and should be used to study business cycles. In his 1972 paper "Expectations and the Neutrality of Money," he creates and analyzes a neoclassical model that displays the Phillips curve, which is a key equation in the
system-of-equations macro models.
But his work is not quantitative dynamic general equilibrium, and only 10 years later did Finn and I figure out how to quantitatively derive the implications of theory and measurement for business cycle fluctuations using the full discipline of general equilibrium theory and national account statistics. That we have learned that business cycles of the quantitative nature observed are what theory predicts is testimony to the grand research program of Ragnar Frisch and to the vision and ingenuity of Robert Lucas. I can think of no paper in economics as important as this one. The key prediction based upon this theoretical analysis—namely, that there is no exploitable trade-off between inflation and employment—was confirmed in the 1970s when attempts were made to exploit the perceived trade-off.
On nearly every dimension, I am in agreement with what Frisch advocated in his Nobel Prize address, but on one dimension I am not. Like Frisch, I am a fervent believer in the democratic process. The dimension where I disagree is how economists and policymakers should interact. His view is that the democratic political process should determine the objective, and economists should then determine the best policy given this objective. My view is that economists should educate the people so that they can evaluate macroeconomic policy rules and that the people, through their elective representatives, should pick the policy rule. I emphasize that Finn and my "Rules Rather Than Discretion" paper finds that public debate should be over rules and that rules should be changed only infrequently, with a lag to mitigate the time consistency problem.
About the Author
In October 2004, Edward C. Prescott, an adviser at the Minneapolis Fed since 1981, received his profession's highest honor, the Nobel Prize in economic sciences. Prescott and his collaborator Finn Kydland were jointly recognized by the Royal Swedish Academy of Sciences for "fundamental contributions to the research area known as macroeconomics. In a highly innovative way, the Laureates have analyzed the design of economic policy and the driving forces behind business cycles." Prescott began work at the Minneapolis Fed after joining the economics department at the University of Minnesota 23 years ago. In addition to work on time inconsistency and business cycle theory, for which he and Kydland were particularly cited by the Swedish Academy, Prescott has done pioneering research in econometric methodology, economic development, finance economics and general equilibrium theory, among other areas. Prescott's Nobel is a capstone in a career marked by many honors, including a Guggenheim fellowship in 1974-75, fellowship in the Econometric Society in 1980 and in the American Academy of Arts and Sciences in 1992, and the Erwin Plein Nemmers Prize in Economics in 2002.
|
Endnotes
1A shortened version of this 1978 Carnegie Mellon working paper, a copy of which I do not have, is a 1980 Northwestern University working paper. At the time, this paper was largely ignored because the profession was not using the neoclassical growth model to think about business cycle fluctuations. But once the then-young people in the profession started using the neoclassical growth model to think about business cycles, the profession found the statistics reported in this paper of interest./p>2 See Stephen M. Stigler's (1978) history of statistics.
3 Rogerson uses the Prescott and Robert M. Townsend (1984a, 1984b) lottery commodity point. This simplifies the analysis, but does not change the results, as lottery equilibria are equivalent to Arrow-Debreu equilibria. (See Timothy J. Kehoe, David K. Levine, and Prescott 2002.)
4 The preference ordering used has a constant elasticity of substitution between consumption and leisure, not between consumption and labor supplied to the market. The elasticity of labor supply for our stand-in household is (1 _ h)/h where h is the fraction of productive time allocated to the market. Given that h is smaller in Europe than one-fourth of the U.S. number, the elasticity of labor supply is even greater than 3 in Europe.
5 Frisch (1970, p. 12) reports that the English mathematician and economist Stanley Jevons (1835-1882) dreamed that we would be able to quantify neoclassical economics.
6 This was further developed by Prescott and Rajnish Mehra (1980). The published version of "Investment Under Uncertainty" did not include the section formally defining the recursive equilibrium with policy and value functions depending on both an individual firm's capacity and the industry capacity and was an industry equilibrium analysis.





